Amdahl's Law

定義 : 針對電腦系統裡面某一個特定的元件予以最佳化，對於整體系統有多少的效能改變

例子 :

方法一: 簡單來說就是全部時間都給我算就對了!

整體的speed up也就是效能的提升 要從兩個面向來看

第一個部分是我們有辦法改進的部分 :

從原本開車換成開飛機

第二個部分是我們沒有辦法改進的部分 :

也就是市區的時間
這些通通都必須要同時列入考量
也因此我們會發現實際的speed up只有2.5倍，而並非是飛機比汽車快4倍

方法二: 比率算法 (看時間的比率)

1代表原本你有做任何改善之前的效能(時間)
在市區的行車時間是沒有辦法被改善的 (而它佔整體的行車時間百分之二十 也就是0.2)
至於在高速公路上面的行車時間是有辦法被改善的
我們可以透過換成改搭飛機 而讓原本的效率快了四倍(時間變成1/4)
也因此整體計算完成之後 我們會發現實際上我們的效能提升是2.5倍

來個有趣的假設 (極限大的提升)

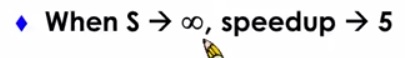
假設飛機的效率是開車的無窮大倍
也就是說飛機可以瞬間從台北到高雄

市區的一個小時依然是沒有辦法被改進的
所以實際上我們我們得到整體效能的提升只有五倍

重要的觀念

如果我們針對系統特定的部分進行效能改變
而想要了解改變了這個部分之後對於整體系統效能的改進是多少
那麼我們需要很清楚的知道
我們改變的部分它 "執行時間佔系統整體執行時間的比率是多少"
同樣的我們 "不能忽略的是我們沒有改變的部分"
也就是沒有加速的部分它的執行時間依然是存在的
依然也會影響到系統整體的執行效能

力氣要花在刀口上

刀口 其實就是我們 改進的這個部分它的執行時間比率佔整體執行時間的比率是多少

如果越高就代表我們的改進對於整體系統的效率提升會比較多 反之 就會比較少

結論 :

我們可以從下面這個式子

1 : 整體時間
F : 可以改變的部分占總時間的比例(時間)
S : F/S 改變後時間變成改變前時間F的 1/S 倍

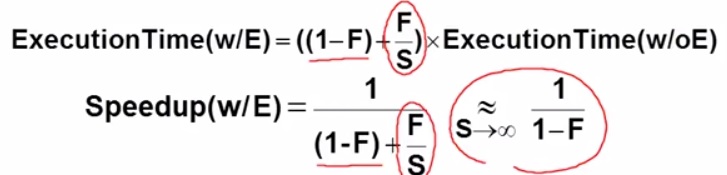
• 我們不可能無窮盡的只提升系統某一個特定部分的效率

  如果我們這麼做，事實上 "最後系統效能的提升是有所極限的"

因為當我們不斷地改進這個系統的某一個特定部分時
這個部分它的執行時間會越來越少 越來越少
以致於即時我們花了更多的力氣
投注在這個部分的效能改進
實際上對於整體的執行時間並沒有太大的幫助